BP（誤差逆伝播法）

概要

  • 勾配法を使うためにNNの目的関数の偏微分を計算するためのアルゴリズム
  • 手順
    • 順伝播: 各層のユニット入出力$\bold{u}, \bold{z}$を正順に計算する
    • 出力層でのデルタ$\delta$を求める
      • 通常は$\delta_j^{(L)} = z_j - d_j$
    • 逆伝播: 中間層でのデルタを逆順に計算していく
      • $\delta_j^{(l)} = \sum_k \delta_k^{(l+1)} \left( w_{kj}^{(l+1)} f'(u_j^{(l)}) \right)$
    • 各層のパラメータ$w$に関する微分を計算する
      • $w_{ji}^{(l)} = \delta_j^{(l)} z_{j}^{(l-1)}$

勾配消失発散問題 (degradation)

  • 順伝播は非線形計算，逆伝播は線形計算
    • デルタの計算は出力層から入力層へ向かって全体が線形
  • デルタの式は積和
    • 各層の重みが大きいとデルタは急速に大きくなり発散する(exploding)
    • 各層の重みが小さいとデルタは急速に小さくなり0になる(vanishing)
    • 隠れ層を増やすほどに学習は難しくなるのは，このせい

事前学習

Residual Network (ResNet)

  • 勾配消失対策（勾配爆発は防げない）
    • $w$の絶対値が小さいと勾配消失が起きる
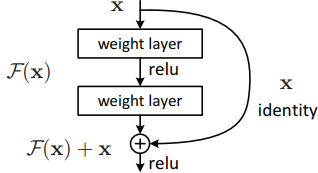
    • $f^{(l+)}(h) = f^{(l)}(h) + h$という関数を構成要素として考える
    • この関数の微分係数は1に近い値になり，誤差が伝播されやすくなる

ResNet

  • 図のようにショートカットをネットワークに導入する

参考文献